How many times have you heard this?
This product has a steep learning curve.
I’ve lost count. But it never ceases to annoy me. What does the above actually mean? And what is the person saying it really trying to get across?
What they’re trying to say: This product is difficult to learn.
What it really means: This product is easy to learn.
Thus you see the confusion, and my frustration. They’re actually saying the opposite of what they meant to say. Usually it’s clear from context what they really mean. But I’m a bit of a stickler when it comes to language issues. (OK, sometimes I’m a lot of a stickler.) So this misuse of the phrase “steep learning curve” really bugs me.
Where does this come from, and why is it so difficult to understand?
My theory is that “steep” seems to connote “difficult”. As in “that’s a steep hill to climb.” But we are not talking about hills, we are talking about curves, and in this case steep means “changing quickly”. And since the curve being discussed is a “learning curve”, that means “can be learned quickly”.
If that explanation makes sense, you can:
- stop reading now
- start using “steep learning curve” properly
- tell other people to do the same
- correct them when they do not
But if you’re not yet convinced, read on. Colleagues of mine from late, lamented XOR in Boulder (you know who you are) will recognize this rant, and the graphs that accompany it.
Learning Curves
To start with, what, exactly, is a learning curve?
I first ran across learning curves in the 70’s. My father brought home a programmable HP calculator (an HP67, as I recall) which was nearly the size of a mechanical adding machine. He wanted to see how this technology could be useful, and since I seemed to have an aptitude for these things (I was in my early teens
at the time, and already showing geekish tendencies) he thought I might be able to put the machine through its paces.
The sample problem my father brought home was to calculate learning curves. Learning curves were part of the toolkit of the reductionist approach that Operations Research practitioners were applying to production line analysis at the time, along with Time-and-Motion studies, Therbligs and other such evil things.
He had a simple formula which related the time required for an individual to perform a task to the number of times that individual had previously performed that task.
T = f ( T0 , Tinfinity , r , n )
That is, the time (T) to perform the task is a function of the time required for an inexperienced user to perform the task the first time (T0), the time required for an experienced user to perform the task
(Tinfinity), the “learning rate” (r), and the number of times it has been performed (n).
The difference between T0 and Tinfinity dictates how much opportunity for improvement there is as a result of having practiced the task many times. That is, some tasks are more amenable to learning from experience than others.
The learning rate parameter encodes the speed with which an inexperienced operator learns and becomes an experienced one. This parameter is the crux of the issue. Its value might change from person to person (some people learn more quickly than others) and from task to task (some tasks can be learned more quickly than others). As I recall there is a sort of “average” value for this parameter that is applicable to the average person and to a wide range of common assembly tasks found on widget assembly lines.
I don’t remember the form of the equation, but I’d be willing to bet it included some sort of negative exponential function that approaches Tinfinity in the asymptote.[1]
What does that all mean? Well here is a picture to help clear things up.
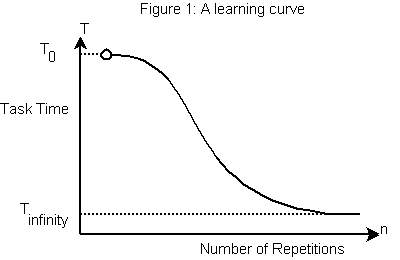
Steep and Shallow Curves
With that background we can start to play with some variations.
The first one, which is directly related to the discussion at hand is the classic “steep learning curve”.
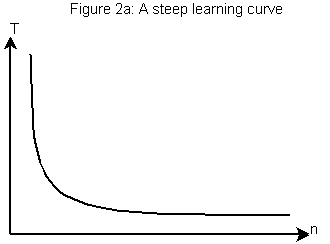
Interpreted verbally: “After only a few iterations, an inexperienced operator is able to perform the task nearly as quickly as a very experienced one.” The widget factory managers like this kind of curve, because it means that when they hire a new assembly line worker, it only takes them a short amount of “training time” before they become as proficient as the other more experienced operators.
What’s the opposite of “steep”? For lack of a better word, I’ll choose “shallow”.
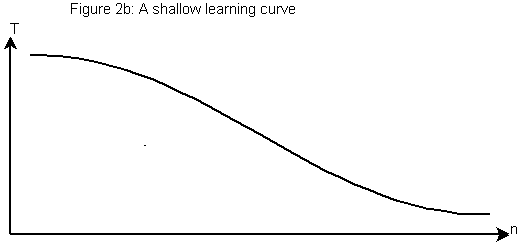
Interpreted verbally: “It takes many iterations before an inexperienced operator reaches the level of proficiency of an experienced one.” The widget factory managers hate this kind of curve, because it means that it is a long time before a new hire is as productive as the existing workforce.
You could also use “gradual”, or “slow” to describe this curve. But I would emphatically not use words like “gentle” or “easy”, as these connote that this is a desirable curve, when this is obviously not the case.
Better terminology
So, if “steep” is confusing and “shallow” isn’t much better, then what is preferable? How about “difficult” and “easy”. As in “This product has a difficult learning curve.” or “This API has an easy learning curve.” I believe I have actually seen this terminology “in the wild”. I wish I had kept a pointer to the reference, so I could send a congratulatory email to the author.
Other Interpretations
When I had this conversation with the XOR folks back in the mid 90’s various objections were raised. They all deserve addressing, to ensure that there is not some interpretation of a learning curve in which “steep” means “good”.
Objection 1: We’re not making widgets
This objection stems from the fact that in most cases in the IT industry these days, the author of the “difficult learning curve” comment is not referring to a repeated activity, but rather to a single, long, drawn-out activity. That is, they are referring to learning to become proficient with a new IDE or API, which is a long and intellectually challenging task, and not to repeating the same mechanical hand-eye-coordination-requiring task over and over.
However, I would argue that the concept maps reasonably well into this new situation. We simply replace the “Number of Repetitions” axis with “Amount of Time Spent with Tool”, and the “Task Time” axis with “Proficiency”.
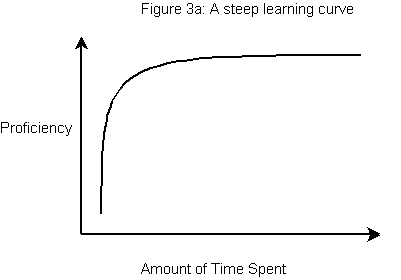
This still looks steep to me. And it still shows that high proficiency is obtained quickly. So “steep” still equals “good”. Objection overruled!
Objection 2: What if the Y axis is reversed?
Figure 3a nicely covers objection 2 as well. As you can see, the value along the Y axis increases over time rather than decreasing. But neither of these changes (relabelling the axes, inverting the Y axis) has changed the fact that this is a steep curve. And the steep curve is still a good one; verbally I would read this curve as “A user new to the tool will rapidly become proficient.” An IT manager would like this kind of tool, since it means that a new hire would become as proficient as the existing coders very quickly.
Just to be sure, let’s also look at a “shallow” (i.e. “not steep”) learning curve with the Y axis inverted.
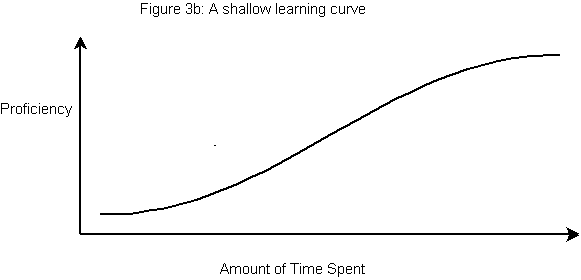
Verbally, it’s clear this graph says: “An inexperienced user will take a substantial amount of time to reach peak proficiency. Our IT manager would be very unhappy with a tool or framework with this sort of learning curve (can you say EJB 1.0/2.0?). So flipping the Y axis hasn’t changed anything. Objection overruled!
Objection 3: What if we measure time spent along the vertical axis?
Cheap answer: “who would do that?”. But OK, I’ll humour you and transpose the axes.
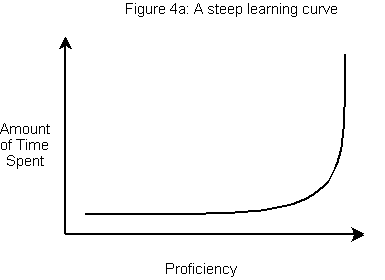
I find this graph hard to read, but if I squint at it, I can see that
- it is steep
- it indicates that high proficiency is reached after a short time
So “steep” is still “good”. This objection also doesn’t change anything. Objection overruled!
Objection 4: Steep means that you have to exert yourself to get up the hill
This objection is harder for me to formulate properly so I can deal with it, but I’ll give it a try. The idea, if I understand it correctly, is that you want to reach a certain proficiency level in a certain amount of calendar time. (Previous graphs have used “Amount of time spent with tool” as the time axis.) The argument here is that, given two different tools, one that is easy to learn and one that is hard to learn, and a goal, say, to be usefully proficient in two weeks, you would have to spend more time and effort learning the more difficult tool in those two weeks to reach equal proficiency. With calendar time as the axis, the two curves now look equally steep, since, by definition, you’ve constrained that to be the same. However this is misleading, as the only reason that the two curves look same is that much more effort was spent learning to use the more difficult tool. The argument here seems to be something like “What we are measuring is the effort required to make the learning curve for any given product look steep.” But what does it mean to compare two products with this interpretation? Under these conditions all curves are as steep or as shallow as you want. So using “steepness” as a comparative in this case is meaningless. We’re back to saying that the tool has a “difficult” learning curve, as in “It’s difficult to make this product’s learning curve into a steep one.” But that hasn’t changed the fact that a steep curve is one on which a user can achieve proficiency in a short period of time. So steepness is still a good thing, not a bad one.
Other Misuses
More Bad Terminology: “Spiky” Learning Curve
I ran across this one just the other day. Some product reviewer said a product had a “spike” in the learning curve. What would he possibly be trying to say? Well, let’s assume he means that you go for a while, learning to use the product, and then you run across something difficult, and you slow down for a while. At least that’s what I got from the context. He implied that spiky learning curves are bad.
If we took him literally, it would mean that the learning curve went up, and then went down again. Note that none of our curves has ever changed direction. Curves that started low and went higher (proficiency as Y axis, which is presumably what this reviewer had as his mental image) never drop back again: they are monotonically increasing. What would it mean if this were not true? It would mean that at some point you become less productive than the day before. This isn’t how learning curves usually work (although… I recall that when the EJB specification first came out my web development productivity went into the toilet for a while… but nevermind).
What this guy is trying to say is that the rate of learning goes through phases where you learn more quickly or less quickly than the average. Notice that magic word “rate”. So he’s really talking about the slope of the learning curve. That is, we have to take the derivative of the learning curve equation.
For a normal learning curve (Figure 5a) a graph of the slope would look approximately like Figure 5b.
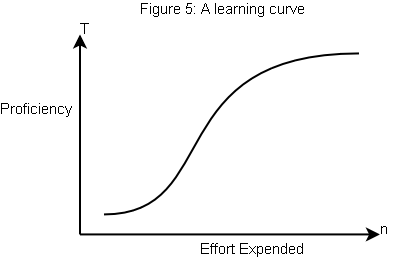
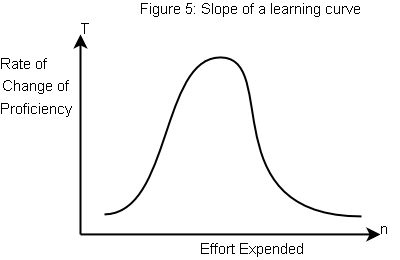
You can clearly see in Figure 5b that there is something resembling a spike: initially you are learning slowly, then you learn quickly for a while, followed by a plateau, where you are proficient, and only small additional gains are possible.
So now we have a mathematical definition of “steep”: the slope or rate of change of the learning curve. Since steep is good, that implies that a large rate of change (or slope) is good, which means that large values on the Y axis of the rate of change graph are good… which means that spiky is good. Spiky means that there are times where you are learning very quickly.
Graphical Error: Billboard
One particularly egregious misuse of learning curves was on a billboard for a local community college I spotted recently. What’s wrong with this picture?

Billboard Caption: “The learning curve of [College X] graduates”
Where do I start? I would read this as “Our graduates are mediocre and never improve.” Not exactly the message the college wants to convey.
How could we help out the college here? What if we replace their bogus graph with Figure 3a, which is our steep learning curve?
Well, there’s a bit of a minefield here, since you could read that graph as “Our graduates don’t know anything but they learn quickly.” Maybe that’s not exactly the message the college wants to convey either.
How about this:
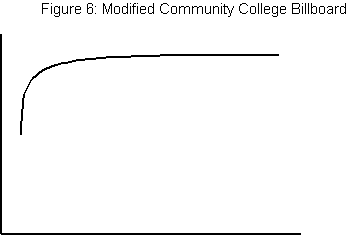
I read this as: “Our graduates know some stuff right out of the program,
and they learn quickly.”
There, problem solved. Now I can sleep at night.
References
[1] The Learning Curve. FAA Acquisition System Toolset.
And did you know that biweekly means BOTH twice a week and every other week. Stomp that one out too.
Tom – you have too much spare time, get a puppy. How about “Lumpy capital”.
Dan Moore writes:
I thought you’d enjoy this article about online poker that uses ‘steep learning curve’ correctly:
Yet it is also part of a trend. Youngsters are flocking to poker as never before, attracted by its growing cachet and the ever-expanding
pots. The plethora of books, blogs and DVDs now easily accessible, and the rapid growth of poker online, means newcomers can learn the art much more quickly than in earlier eras. “When I started out it took years of hard grind at the table to get good. Now the learning curve is much steeper,” says Howard “The Professor” Lederer, a professional player.
It is often said that while Texas Hold ‘Em, the most popular version of poker, may take only minutes to learn, it takes a lifetime to master. Annette_15 may beg to differ.
http://economist.com/displaystory.cfm?story_id=10281315